谷歌大脑提出AutoML-Zero,目前代码已开源
AlphaGo战胜了人类最强棋手,但前提是它先学会了人类棋谱,离不开人类指导。
接着谷歌又推出了AlphaGo Zero,只让AI知道围棋规则,从零开始学下棋,结果再次登上棋艺顶峰。
AI既然能从零学习围棋,是否可以从零开始摸索机器学习算法?当然可以,谷歌大脑团队最新的研究成果已经做到了。
谷歌将这种技术称之为 AutoML-Zero,意为“从零开始的自动机器学习”,已经在GitHub开源,并在Arxiv上提交了论文。

而且这一研究还是来自谷歌大脑的Quoc V.Le大神之手。
AutoML-Zero仅使用基本数学运算为基础,从一段空程序开始,即可自动发现解决机器学习任务的计算机程序。
AutoML Zero能发现什么
AutoML是一种实现从数据集到机器学习模型的自动化方法,让你无需高深专业知识,就能自动部署ML模型。
虽说是自动,但现阶段的AutoML还要对搜索空间进行很大的限制,这使我们在使用AutoML的时候仍然需要一些专业知识去设计神经网络的层。
谷歌的目标是让AutoML可以走得更远,仅仅使用基本的数学运算作为构建块,就可以自动发现完整的机器学习算法,进一步降低机器学习的门槛。

尽管AutoML-Zero巨大的搜索空间充满挑战性,但进化搜索还是能发现具有梯度下降的线性回归算法、具有反向传播的二层神经网络。
值得注意的是,可以AutoML-Zero的进化过程也是一个不断“发明”的过程解释进化的算法,它已经找到了双线性交互、权重平均、归一化梯度、数据增强等技术,甚至在某些情况下还发现了类似Dropout的算法。
下面我们先来看看,AutoML在CIFAR-10的二元分类任务上是如何一步步进化的。它首先发现了线性回归,然后找到了损失函数、梯度下降。
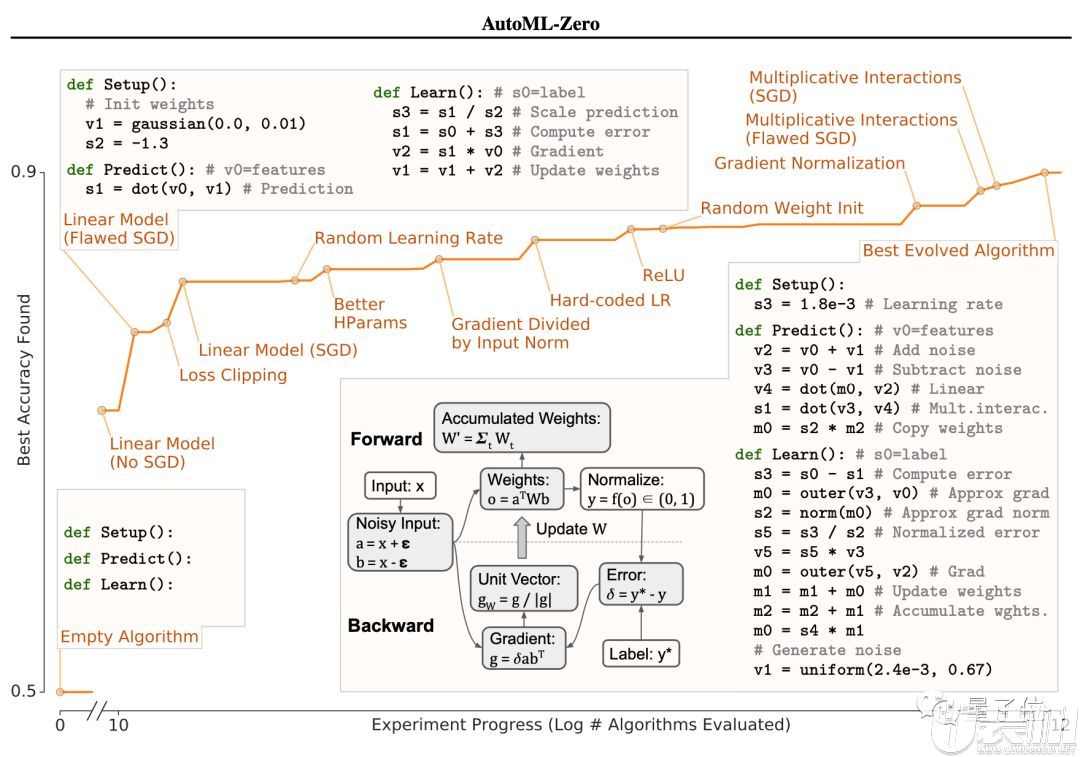
随着训练的进行,出现了随机学习率、随机权重、激活函数ReLU、梯度归一化,最后得到了84.06 ± 0.10%正确率的终极算法。
只训练一个二元分类结果还不太具有说服力,作者又用3种极端情况考察了Auto ML。
首先,当样本数量很少的时候,在80个样本上运行100个epoch。AutoML竟然进化出另一种适应性算法,给输入数据加上了噪声,并开始使用Dropout来训练模型。
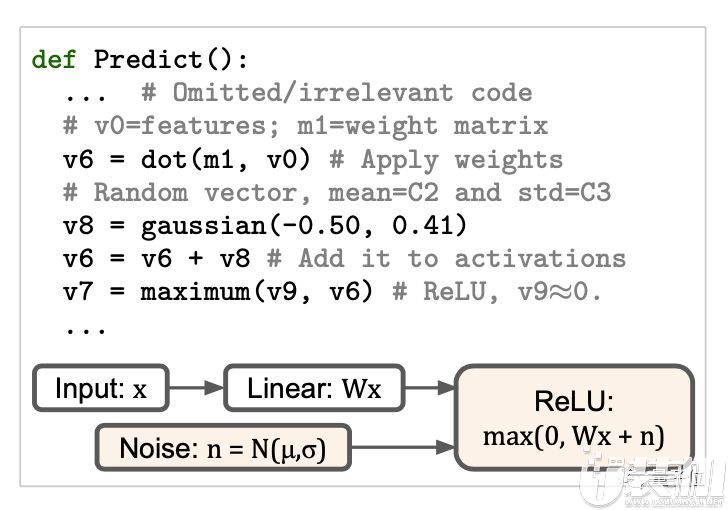
在快速训练的情况下,只有800个样本和10个epoch,结果导致学习率衰退反复出现,这
是一个我们在快速训练训练机器学习模型中常见的策略。
至于多类别的分类问题,作者使用了CIFAR-10数据集的所有10个类。AutoML进化算法有时会使用权重矩阵的变换平均值作为学习速率。甚至作者也不知道为什么这种机制会更有利于多类任务,虽然这种结果在统计学上是显著的。
上面的所有测试整个过程中,人类没有告诉程序任何先验的机器学习知识。
演示
现在谷歌将AutoML-Zero的程序提交到GitHub,普通电脑只需5分钟就能体验一 下它的实际效果。
安装好Bazel后,将代码下载到本地,运行其中的demo程序:
git clonehttps://github.com/google-research/google-research.git
cdgoogle-research/automl_zero
./run_demo.sh
这个脚本在10个线性任务上运行进化搜索。每次实验后,它都会评估在100个新的线性任务中发现的最佳算法。一旦算法的适应度大于0.9999,就选择该算法作为最终结果,将代码打印在屏幕上。
在普通电脑上使用CPU在5分钟内就能发现类似于梯度下降进行线性回归的程序:
found:
defSetup:
s3 = -0.520936
s2 = s2 * s3
s2 = dot(v1, v1)
v2 = s2 * v1
s2 = s3 * s2
v1 = s0 * v2
s2 = s0 - s3
s2 = -0.390138
v2 = s2 * v0
s1 = dot(v1, v0)
defPredict:
s2 = -0.178737
s1 = dot(v1, v0)
defLearn:
s1 = s1 * s2
s3 = s3 * s2
s2 = s0 * s2
s1 = s1 - s2
v2 = s1 * v0
v1 = v2 + v1
v2 = s3 * v0
v1 = v2 + v1
由人工设计的ML算法是,有兴趣的话,你可以比较这两段程序的差异。
defSetup:
s2 = 0.001# Init learning rate.
defPredict: # v0 = features
s1 = dot(v0, v1) # Apply weights
defLearn: # v0 = features; s0 = label
s3 = s0 - s1 # Compute error.
s4 = s3 * s1 # Apply learning rate.
v2 = v0 * s4 # Compute gradient.
v1 = v1 + v2 # Update weights.



















